Conditional Postural Synergies III: Grasp pose sampling

In the two previous posts, we focused primarily on finger control. We explored the representation and generation of grasp postures based on high-level properties and we developed a force feedback controller to grasp and release objects. However, the initial step in any manipulation task is to initially grasp the target object. This usually means providing the robot with both a grasp pose, which specifies the position and orientation of the end-effector, and a grasp posture, i.e. the finger configuration.

In this post, we will explore how to sample grasp poses with respect to objects, i.e. hand positions and rotations, in order to execute several precision grasps. The main idea behind our approach (Dimou et al. 2022), is to factor the grasp sampling process into a set of cascaded steps. More specifically, our proposed system consists of three separate models that generate a grasp posture, using the postural synergies framework developed in the first post, and a position and an orientation for the hand. Each model is conditioned on the outputs of the previous one. The models are trained separately on a dataset of successful grasp samples that are computed using a geometric heuristic.

Grasp sampling

Generally, grasp sampling approaches are divided into analytical and data-driven methods (Sahbani et al. 2012). Analytical approaches use a model of the object and optimize a grasp quality metric in order to find the optimal contact points. They require accurate contact modeling and the definition of cost functions, while the optimization process can be time-consuming and subject to local optima. On the other hand, data-driven approaches (Bohg et al. 2013) rely on large datasets of successful grasp examples, which are used to train models to either: 1) approximate some success metric such as the probability of successfully grasping an object, 2) directly generate a candidate grasp using some kind of generative model.

We adopt a data-driven approach since we believe that is more appropriate for real-world applications. So our first goal is to collect a dataset of successful grasp examples for each grasp type and object. To achieve this we design a geometric heuristic to compute candidate grasps which we execute in simulation and collect the successful ones. We, then, train each model on the collected dataset and, finally, we sequentially sample from each model to generate new grasps.

Data Collection

To get a successful grasp we first generate a candidate grasp posture by sampling from a trained CVAE model, similar to the one presented in the previous posts. This model is exclusively employed during the data generation process and is subsequently discarded. We generate grasps belonging to one of the following six precision grasp types: tripod, palmar pinch, parallel extension, writing tripod, lateral tripod, and tip pinch.

After we have a candidate grasp posture, we compute a candidate hand position. In practice, we assume that the hand remains fixed at the origin of the coordinate axis, and we calculate the candidate position for the object within the hand’s reference frame. To compute the candidate object position we leverage the inherent structure precision grasps (Iberall & MacKenzie 1990).

Precision grasps rely on the opposition between specific finger joints, known as opposition joints, to achieve stability. In particular, the thumb and index fingers are commonly used to create what is known as pad opposition. The axis connecting these finger segments is referred to as the opposition axis. For each grasp posture, we have a pair of opposition joints that results from the grasp type’s structure, as well as an opposition axis that depends on the geometric arrangement of the physical finger segments responsible for the opposition.

Based on the selected opposition joints for the given grasp type, we employ forward kinematics to determine the Cartesian positions of the two rigid bodies associated with these joints during the execution of the grasp and compute their middle point. We then set the center of mass of the object to that middle point, as it is often observed that humans tend to grasp objects near their center of mass to enhance stability, especially when using precision grasps. To find a candidate object rotation we simply align one of the three canonical axes of the object with the opposition axis.

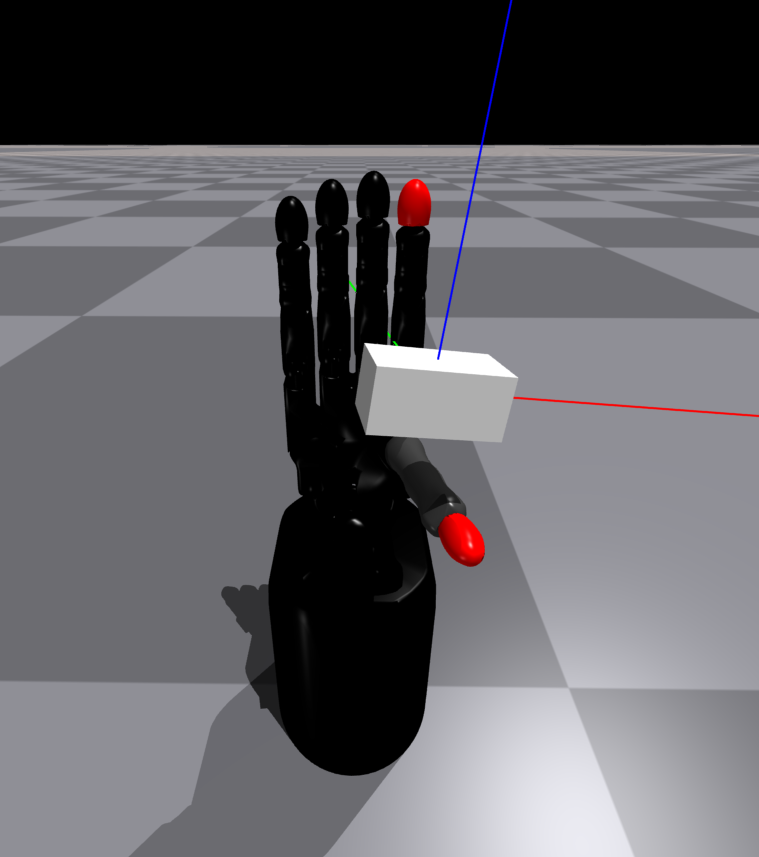
Finally, the object is positioned according to the calculated pose, and the grasp is executed. We then shake the hand to filter out any unstable grasps and we activate gravity. If the object remains in the hand for 5 seconds after gravity is activated, the grasp is considered successful. At this point, several values such as the grasp type, the grasp size, etc. are recorded. We perform this procedure using Nvidia's IsaacGym simulator which allows us to run in parallel multiple environments. This way we can collect a large dataset of successful grasps in a matter of hours.

Proposed Model

Our primary objective is to develop a model of the distribution of successful grasps $P (G \mid C)$, where $G = (G_c, G_{pos}, G_{rot})$ represents a successful grasp, consisting of the grasp configuration $G_c$, represented by the finger joint angles, the 3D position $G_{pos}$, and the 6DoF rotation $G_{rot}$ of the hand and $C$ represents the properties of the grasp and the object.

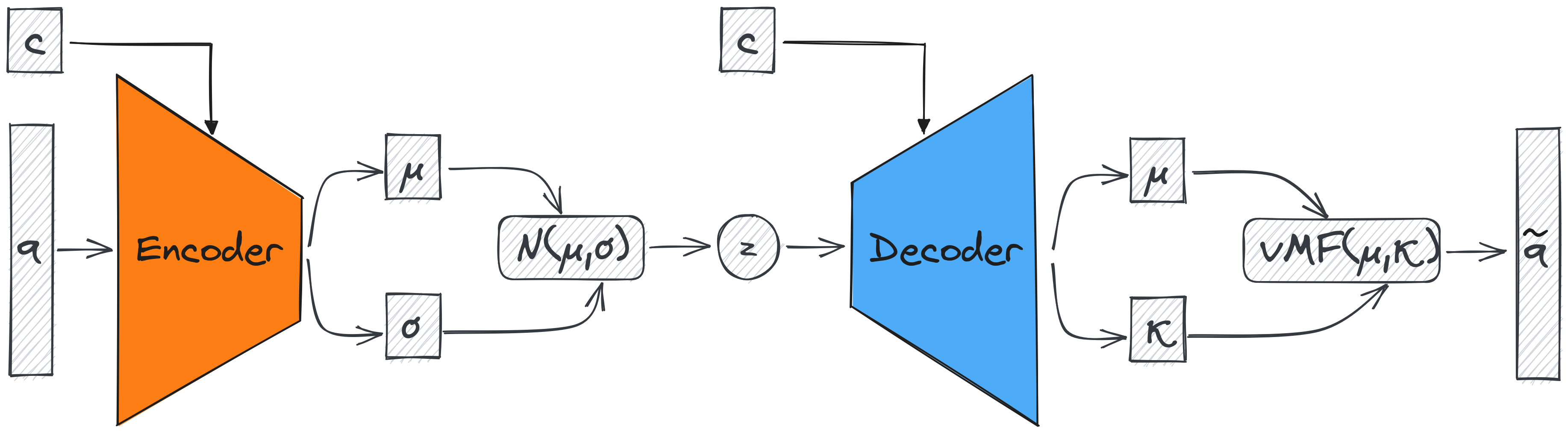
In contrast to previous works that directly modeled the full distribution: $$ P (G \mid C) = P (G_c, G_{pos}, G_{rot} \mid C),$$ we adopt a different approach by factorising the distribution in its three components. Specifically, we train three individual samplers: the Posture Sampler, the Position Sampler, and the Rotation Sampler, each employing a CVAE architecture. The Posture Sampler models the probability distribution: $$ P(G_c \mid C),$$ which represents the finger configuration of the grasp and is indicated by the angle values for each finger joint. The Position Sampler models the probability distribution: $$ P (G_{pos} \mid G_c, C)$$ which represents the 3D position of the hand w.r.t the object. Finally, the Rotation Sampler models the probability distribution: $$ P(G_{rot} \mid G_c, G_{pos}, C)$$ which represents the rotation of the hand using quaternions. Instead of using directly the output of the CVAE to model the rotation, the Rotation Sampler generates the mean direction $\mu$ and concentration parameter $\kappa$ of a von Mises-Fisher distribution whose samples are constrained to lie on the unit sphere (Sra, S. 2016). In practice, we use a differentiable implementation of the von Mises-Fisher distribution (Davidson et al. 2018), to be able to apply gradient descent to train the model. Finally, the rotation of the hand is sampled from the learned von Mises-Fisher distribution. A graphical example of our model is shown in the following figure.

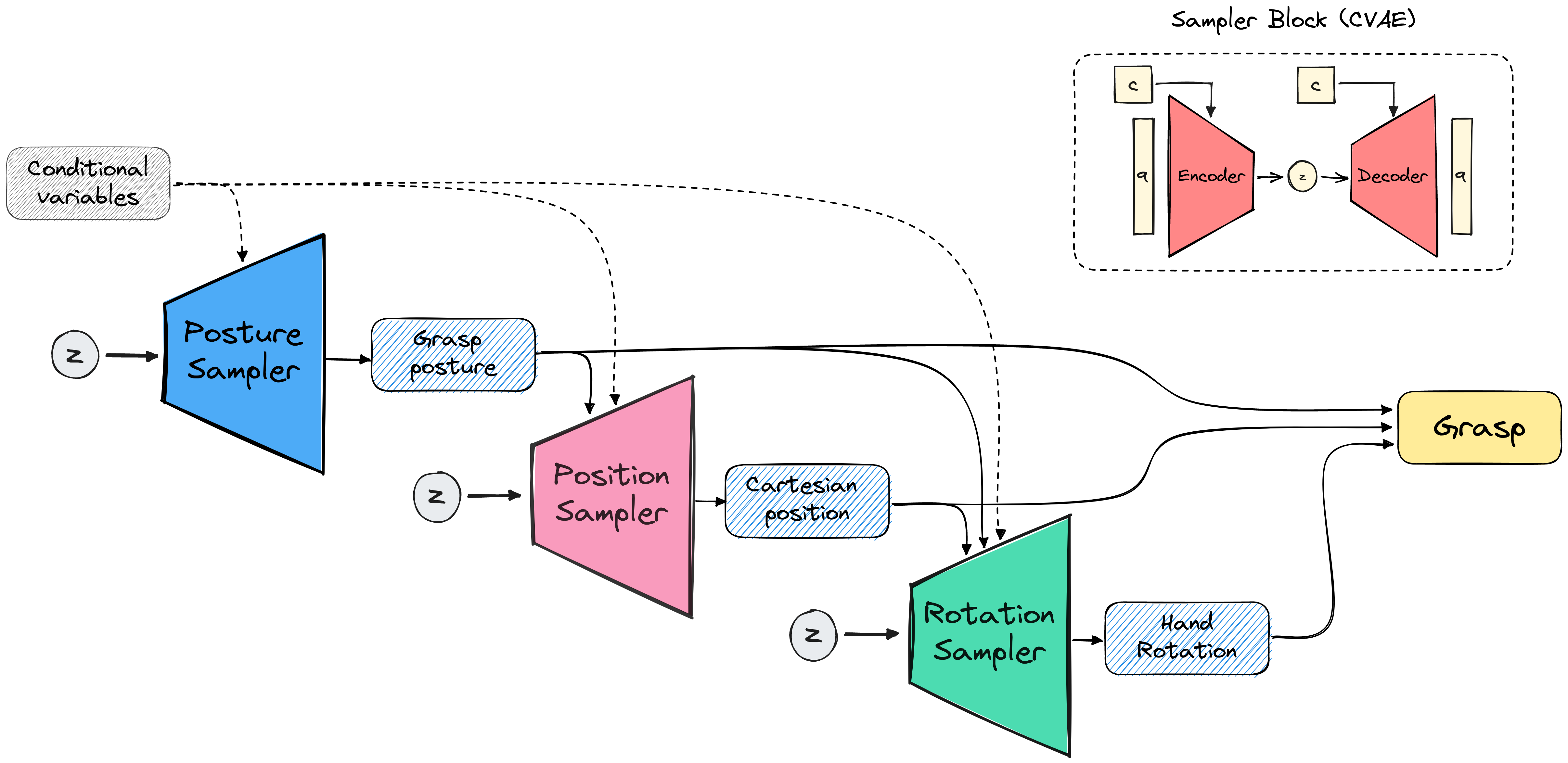
To obtain grasp samples from the model, first, we sample a latent point from the prior distribution of the Posture sampler, and along with the corresponding conditional variables we feed them to the decoder of the model to generate a grasp posture. Then we perform the same procedure for the Position and Rotation samplers, each time adding the output of the previous models to the conditional variables. Finally, the generated grasp posture, hand position, and hand rotation form a complete grasp.

Results

To test our hypothesis that factorizing the grasp into its components better models the grasp distribution, we compared our proposed model against using a single model to generate all modalities, as well as using two models, one for grasp postures and another for poses (position and rotation). The factorized model exhibited superior performance in terms of grasp success rate. In addition, we compared several variants of the factorized model to conclude which were the best conditional variables to use, as well as to determine if using the von Mises-Fisher distribution to represent rotations was better than directly using the output of the CVAE. More details on our experiments can be found in our paper.

To employ our model in practical grasping tasks such as object pick-up, we assume that the pose of the object is given by the perception system. We then sample a grasp using our model, which is essentially the object pose in the reference frame of the hand and transform it to the reference frame of the object. We then check if there are no collisions with the environment and execute the grasp, i.e. command the finger joint angles. In the Figures below you can see some example grasps.

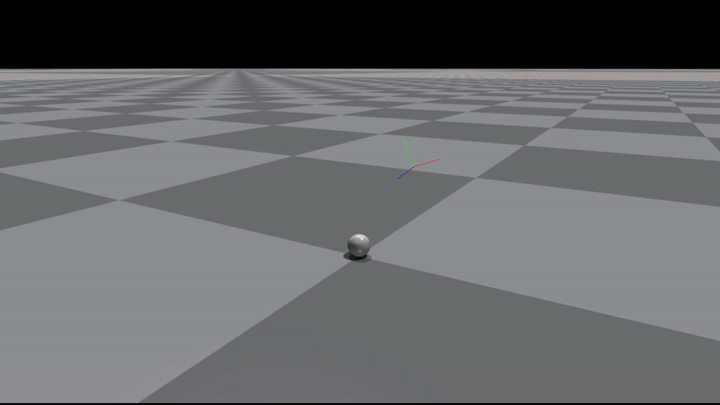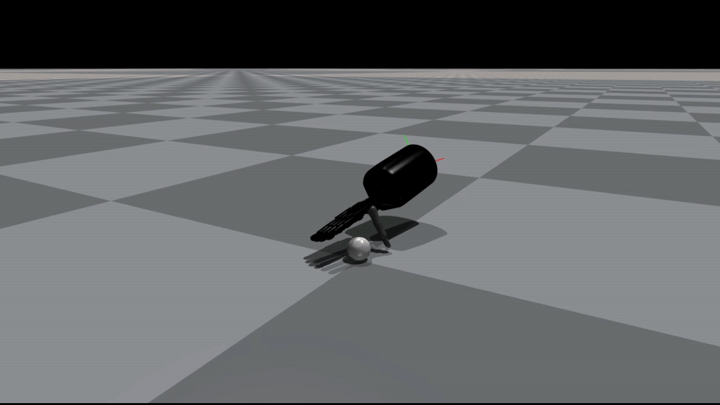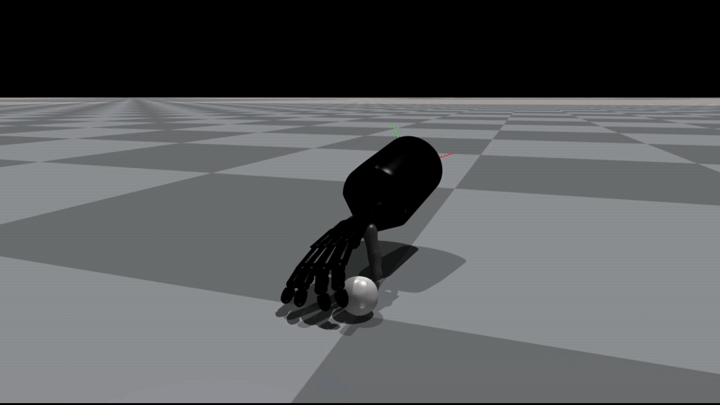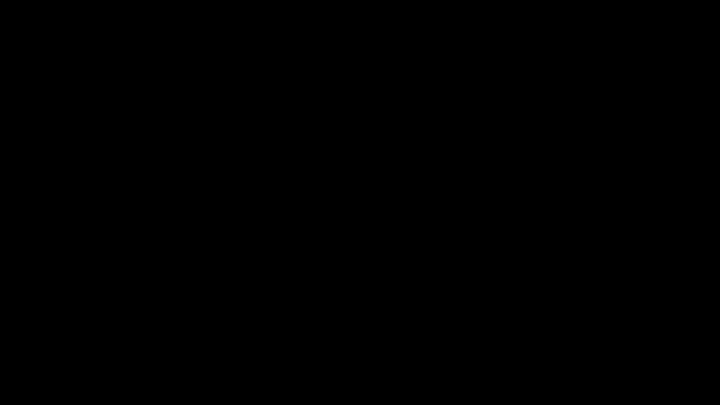
Conclusion

In summary, we developed a factorized model to sample dexterous grasps for explicitly executing precision grasps. Our model employs three cascaded samplers: one for the finger configuration, one for the hand position, and one for the hand rotation, where each sampler is implemented using a CVAE. The model is trained on a dataset of successful grasp examples collected using a geometric heuristic in simulation.

References

[1] Dimou et al. “Grasp Pose Sampling for Precision Grasp Types with Multi-fingered Robotic Hands.” Humanoids, 2022.

[2] Sahbani et al. “An overview of 3D object grasp synthesis algorithms.” Robotics and Autonomous Systems, 2012.

[3] Bohg et al. “Data-Driven Grasp Synthesis—A Survey.” Transactions on Robotics, 2013.

[4] Iberall & MacKenzie "Opposition space and human prehension." Springer, 1990.

[5] Sra, S. "Directional Statistics in Machine Learning: A Brief Review." Applied Directional Statistics, 2016.

[6] Davidson et al. "Hyperspherical Variational Auto-Encoders." Uncertainty in Artificial Intelligence, 2018.